4.3.1.2 Predicting Asset Performance

Predicting Asset Performance

A life cycle strategy is enhanced by the availability of models and analysis tools that facilitate the evaluation of different combinations of treatment type and timing across the asset class. For this analysis a model that predicts future asset deterioration and response to treatments is required.

For condition-based approaches to managing assets, historical performance is typically used as a baseline for developing models to predict future performance. The predicted conditions are used to determine the type of treatments that may be needed over an asset’s service life, so the ability to accurately predict asset conditions in the future, with and without treatment, is an essential component of asset management. Models are developed by comparing performance, typically measured as asset condition, over time with actions or treatments performed on specific assets. This means that performance is associated to the last action or treatment that impacted performance in a positive way. However, assets may also receive treatments that delay the onset or advancement of distress. As a result, most models assume assets receive some level of preventive or routine maintenance between more significant treatments. If agency practices change to delay or cease maintenance activities, assets may not perform as models predict.

Several methods can be used to estimate future asset performance, the two most
common of which, deterministic and probabilistic, are described below. Additional information has been published by NCHRP (Report 713, 2012 ): Estimating Life Expectancies of Highway Assets. This report also contains guidance on selecting the most appropriate modeling approach for various highway asset classes.

Deterministic Modeling

Deterministic modeling is a common and relatively simple approach for using historic data to predict future asset performance. Deterministic models apply regression analysis to one or more independent variables, typically condition over time, and develop a “best-fit” equation to determine the rate at which asset conditions change. The independent variables are used to predict a single dependent variable, most commonly represented as the predicted condition at some point in time in asset management applications. Developing deterministic models is relatively easy but relies on quality data collected consistently over several years to produce dependable results. Deterministic models are more easily implemented as they are more readily paired with linear program solving. They also provide consistent outputs. The downside of deterministic models is the limited insight that they provide into the cost uncertainty surrounding a strategy.

Probabilistic Modeling

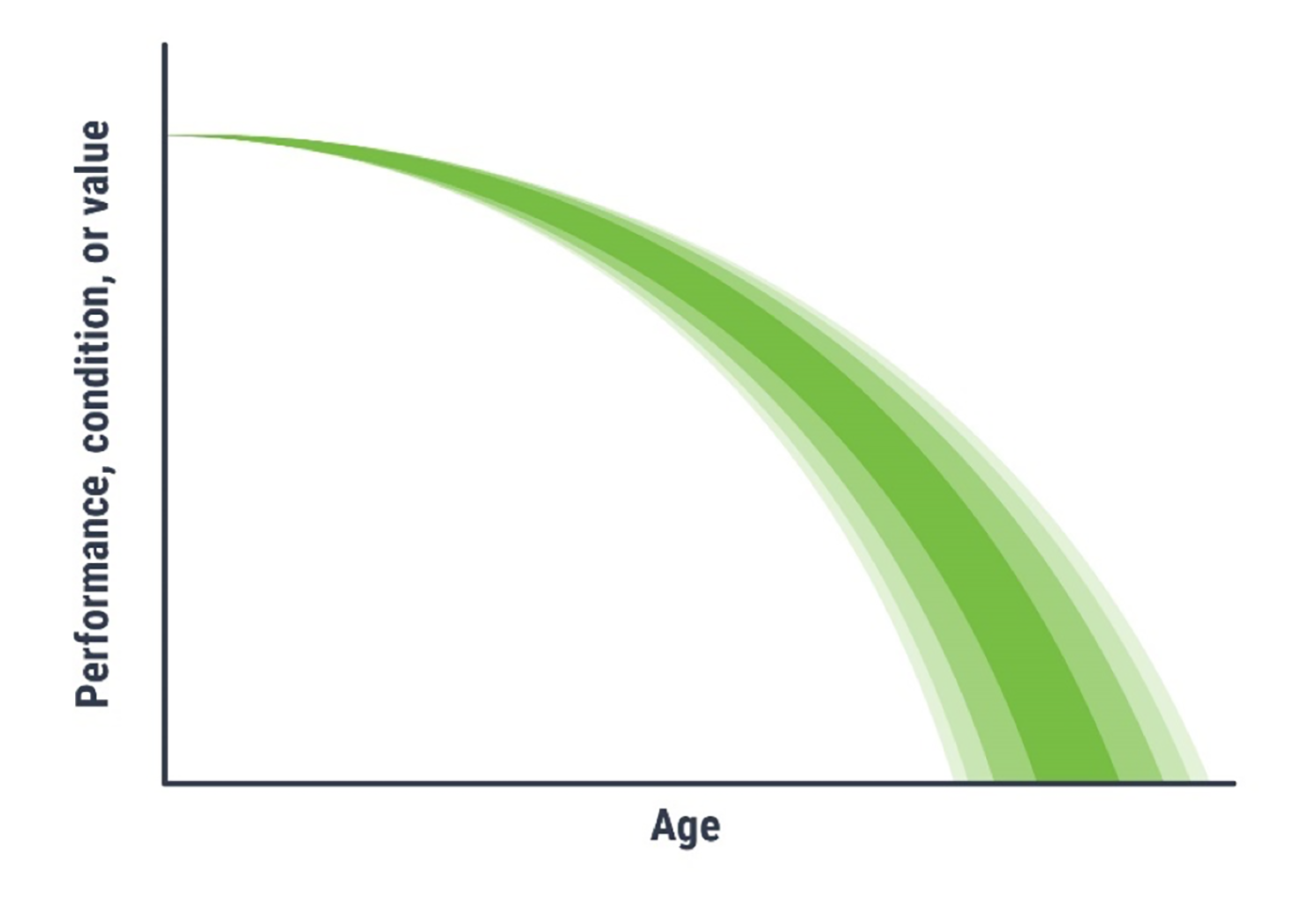
Unlike deterministic models, which provide a single repeatable outcome, probabilistic models provide a distribution of possible strategies that provides insight into the cost uncertainty of plans. Probabilistic models can also more readily accept uncertainty in other variables, as represented by the shading in Figure 4.7. Given that condition changes are probabilistic, no two strategies that the model will provide are the same. This means that multiple iterations of the model with the same inputs can provide different results. Accordingly, probabilistic models are useful for setting funding limit expectations, while deterministic models help to provide insights into which projects are best to apply to specific assets.

Common approaches to developing probabilistic models are the Markov, Semi-Markov and Weibull models. Markov modeling works well for assets with condition ratings based on regular inspections. There are several ways of establishing a Markov model, but the simplest is to calculate the proportion of assets that change from one condition state to the next in any given year. These proportions are then used to develop what is known as the transition matrix. At the start of the model run, an asset “knows” its condition state. Once this is known there is then a probability it will change from its current condition state to the next in any given year. While these types of Markov approaches have been widely used, they do not necessarily model deterioration effectively, as the rate of change of condition increases with time. To address this, Semi-Markov models are used. Like Markov, Semi-Markov models have a condition transition matrix, but this is also augmented with a time selection matrix. In these models the probability of a condition jump is calculated, then the length of time an asset will remain in that condition state is also selected. Using more advanced mathematical techniques, the Semi-Markov approach can be expressed similarly to the Markov approach, but for Semi-Markov, the transition matrix changes with time. This reflects the increasing likelihood the asset will transition (deteriorate faster as its ages). Such models are typically used on long-lived assets.

A Weibull model offers another approach for modeling asset deterioration. A Weibull distribution predicts the likelihood of asset failure or deterioration as a function of age. Weibull models are particularly useful for addressing assets rated on a pass/fail basis during inspection. The Weibull model provides an additional factor meant to address the increasing or decreasing likelihood of an asset moving from an acceptable to an unacceptable state between inspection cycles. Reliability is the inverse of the probability of failure (i.e. 1 -p(f)). Reliability, like Weibull can thus be used to assess the likelihood an asset will provide the required service. The relationship between time and reliability is assessed by analyzing asset behavior to understand potential modes of failure. This analysis is a core aspect of reliability-centered maintenance, and is more typically used on short lived assets.